BFS和DFS

2021-01-12

BFS

填涂颜色

题目描述
由数字00组成的方阵中，有一任意形状闭合圈，闭合圈由数字11构成，围圈时只走上下左右44个方向。现要求把闭合圈内的所有空间都填写成22.例如：6 \times 66×6的方阵（n=6n=6），涂色前和涂色后的方阵如下：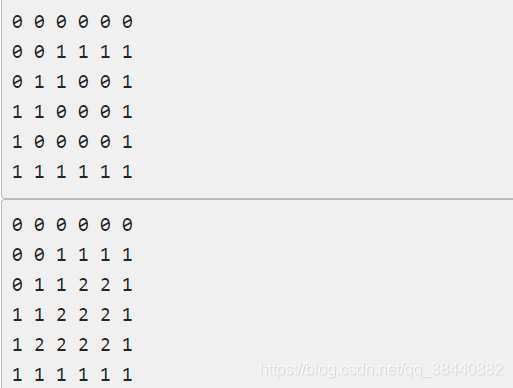
在这里插入图片描述
输入格式
每组测试数据第一行一个整数n(1≤n≤30)
接下来n行，由0和1组成的n×n的方阵。
方阵内只有一个闭合圈，圈内至少有一个0。

输出格式
已经填好数字22的完整方阵。

输入

6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1

输出

0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1

#include<iostream>
#include<queue>

using namespace std;
const int MAXN=100;
int Map[MAXN][MAXN];
int vis[MAXN][MAXN];//访问标记，为0表示没被访问
//能走的四个方向
int way[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
struct position{
    int x,y;
    position(int x,int y):x(x),y(y){};
};
queue<position> q;
int main(){
    int n;
    cin>>n;
    //最开始应该在外面再加一圈零(从1开始输入),因为(0,0)这个点若是1就完蛋
    //所以要注意遍历初始点的选取
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>Map[i][j];
        }
    }
    q.push(position(0,0));//初始点进队列
    vis[0][0]=1;
    while(!q.empty()){
        position current=q.front();
        for(int i=0;i<4;i++){
            //沿着每个方向变化后的横纵坐标
            int x=current.x+way[i][0];
            int y=current.y+way[i][1];
            //cout<<x<<" "<<y<<endl;
            //加了Map[x][y]==0的条件，将1围成的圈外部的0全部置已访问
            if(x>=0&&x<=n+1&&y>=0&&y<=n+1&&Map[x][y]==0&&vis[x][y]==0){
                q.push(position(x,y));
                vis[x][y]=1;
            }
        }
        q.pop();
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(Map[i][j]==0&&vis[i][j]==0){
                cout<<2<<" ";
            }
            else  cout<<Map[i][j]<<" ";
        }
        cout<<endl;
    }
}

马的遍历

题目描述
有一个n*m的棋盘(1<n,m<=400)，在某个点上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步

输入格式
一行四个数据，棋盘的大小和马的坐标

输出格式
一个n*m的矩阵，代表马到达某个点最少要走几步（左对齐，宽5格，不能到达则输出-1）

输入

3 3 1 1

输出

0 3 2
3 -1 1
2 1 4

#include<iostream>
#include<queue>
#include<cstdio>
using namespace std;
const int MAXN=500;
int Map[MAXN][MAXN];
int vis[MAXN][MAXN];
struct position{
    int x,y;
    int steps;
    position(int x,int y,int steps):x(x),y(y),steps(steps){};
};
//马跳的8个方向
int way[8][2]={{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}};

queue<position> q;
int main(){
    int n,m,x1,y1;
    cin>>n>>m>>x1>>y1;
    q.push(position(x1-1,y1-1,0));//初始点
    vis[x1-1][y1-1]=1;//这一步别忘了
    while(!q.empty()){
        position current=q.front();
        for(int i=0;i<8;i++){
            int x=current.x+way[i][0];
            int y=current.y+way[i][1];
            if(x>=0&&x<=n-1&&y>=0&&y<=n-1&&vis[x][y]==0){
                q.push(position(x,y,current.steps+1));
                Map[x][y]=current.steps+1;
                vis[x][y]=1;
            }
        }
        q.pop();
    }
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(vis[i][j]!=0) printf("%-5d",Map[i][j]);
            else printf("%-5d",-1);
        }
        cout<<endl;
    }
}

奇怪的电梯

题目描述
呵呵，有一天我做了一个梦，梦见了一种很奇怪的电梯。大楼的每一层楼都可以停电梯，而且第ii层楼(1≤i≤N)上有一个数字Ki(0≤Ki≤N)。电梯只有四个按钮：开，关，上，下。上下的层数等于当前楼层上的那个数字。当然，如果不能满足要求，相应的按钮就会失灵。例如：3, 3 ,1 ,2 ,5代表了Ki(K1=3,K2=3,…)，从1楼开始。在1楼，按“上”可以到4楼，按“下”是不起作用的，因为没有−2楼。那么，从A楼到B楼至少要按几次按钮呢？

输入格式
共二行。
第一行为3个用空格隔开的正整数，表示N,A,B(1≤N≤200, 1≤A,B≤N)。
第二行为N个用空格隔开的非负整数，表示Ki

输出格式
一行，即最少按键次数,若无法到达，则输出−1。

输入

5 1 5
3 3 1 2 5

输出

3

#include<iostream>
#include<queue>

using namespace std;
struct sta{
    int f;
    int steps;
    sta(int f,int steps):f(f),steps(steps){};
};
const int MAXN=300;
int way[MAXN];//记录可以移动的步数
int vis[MAXN];
queue<sta> q;
int main(){
    int n,a,b;//a为起点,b为终点
    cin>>n>>a>>b;
    for(int i=1;i<=n;i++){
        cin>>way[i];
    }
    q.push(sta(a,0));
    vis[a]=1;
    while(!q.empty()){
        sta current=q.front();
        //cout<<current.f<<endl;
        if(current.f==b){//出口
            cout<<current.steps<<endl;
            return 0;
        }
        int down=current.f-way[current.f];//向下
        if(down>=1&&vis[down]==0){
            q.push(sta(down,current.steps+1));
            vis[down]=1;
        }
        int up=current.f+way[current.f];//向下
        if(up<=n&&vis[up]==0){
            q.push(sta(up,current.steps+1));
            vis[up]=1;
        }
        q.pop();
    }
    cout<<-1<<endl;
}

01迷宫

题目描述
有一个仅由数字0与1组成的n×n格迷宫。若你位于一格0上，那么你可以移动到相邻4格中的某一格1上，同样若你位于一格1上，那么你可以移动到相邻4格中的某一格0上。
你的任务是：对于给定的迷宫，询问从某一格开始能移动到多少个格子（包含自身）。

输入格式
第1行为两个正整数n,m。
下面n行，每行n个字符，字符只可能是0或者1，字符之间没有空格。
接下来m行，每行2个用空格分隔的正整数i,j，对应了迷宫中第i行第j列的一个格子，询问从这一格开始能移动到多少格。

输出格式
m行，对于每个询问输出相应答案。

输入

2 2
01
10
1 1
2 2

输出

4
4

#include<iostream>
#include<queue>

using namespace std;
const int MAXN=2000;

struct position{
    int x,y;
    position(int x,int y):x(x),y(y){};
};
int Map[MAXN][MAXN];
int vis[MAXN][MAXN];
int ans[10000000];//存的是各个颜色区域的结点数
int color=0,n,m;
int way[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
queue<position> q;
void bfs(int x1,int y1){
    int cnt=0;//用来对当前颜色的区域来计数
    q.push(position(x1,y1));
    vis[x1][y1]=color;
    while(!q.empty()){
        position current=q.front();
        //cout<<current.x<<" "<<current.y<<endl;
        for(int k=0;k<4;k++){
            int x=current.x+way[k][0];
            int y=current.y+way[k][1];
            if(x>=1&&x<=n&&y>=1&&y<=n&&vis[x][y]==0&&Map[x][y]!=Map[current.x][current.y]){
                q.push(position(x,y));
                vis[x][y]=color;
            }
        }
        cnt++;
        q.pop();
    }
    //cout<<color<<endl;
    ans[color]=cnt;
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            char c;
            cin>>c;
            Map[i][j]=c-'0';
            //cout<<Map[i][j]<<endl;
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(vis[i][j]==0){
                color++;//每一个color来区分一块互相可以到达的区域
                //cout<<color<<endl;
                bfs(i,j);//注意函数中不能出现i,j
            }
        }
    }
    for(int i=1;i<=m;i++){
        int xx,yy;
        cin>>xx>>yy;
        cout<<ans[vis[xx][yy]]<<endl;
    }


}

墙与门

在这里插入图片描述
注:这是一道多源bfs的题，将终点看做第0层，然后逐层遍历

int way[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
    void wallsAndGates(vector<vector<int>>& rooms) {

        int m=rooms.size();
        if(m==0) return;
        int n=rooms[0].size();
        vector<vector<int>> vis(m,vector<int>(n,0));
        queue<pair<int,int>> q;
        //将第0层的所有结点push进队列
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(rooms[i][j]==0){
                    vis[i][j]=1;
                    q.push({i,j});
                }
            }
        }
        //q一直保存当前层以及下一层的结点(除了在最开始只保存第0层的结点)
        int step=0;
        while(!q.empty()){
            int k=q.size();
            step++;
            while(k--){

                for(int i=0;i<4;i++){
                    int xd=q.front().first+way[i][0];
                    int yd=q.front().second+way[i][1];
                    if(xd>=0&&xd<m&&yd>=0&&yd<n&&vis[xd][yd]==0&&rooms[xd][yd]!=-1){
                        vis[xd][yd]=1;
                        rooms[xd][yd]=step;
                        q.push({xd,yd});
                    }
                }
                q.pop();
            }
        }
    }

DFS

八皇后问题

题目描述
一个如下的6×6 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。
在这里插入图片描述
上面的布局可以用序列2 4 6 1 3 5 来描述，第 i 个数字表示在第 i 行的相应位置有一个棋子，如下：
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。

输入格式
一行一个正整数 nn，表示棋盘是 n \times nn×n 大小的。

输出格式
前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入

6

输出

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

#include<iostream>
#include<cstdlib>
using namespace std;
int ans[13];//作为每次深搜出来的序列的结果
int vis[13];
int u[40];//正对角线
int v[40];//副对角线
int n;
int Count=0;
void print(){
    for(int i=1;i<=n;i++){
        cout<<ans[i]<<" ";
    }
    cout<<endl;
}

void dfs(int x){//dfs中的参数是行号
    if(x>n){
        Count++;
        if(Count<=3) print();
        return ;
    }
    for(int i=1;i<=n;i++){//i表示尝试列号
        if(!vis[i]&&!u[x-i+n]&&!v[x+i]){//vis能保证不在同一列,u表示不在同一主对角(+n为了不为负数),v表示不在同一副对角
            //i-ans[j]为列差,x-j为行差
            vis[i]=1;
            u[x-i+n]=1;
            v[x+i]=1;
            ans[x]=i;
            dfs(x+1);
            //为了回溯
            vis[i]=0;
            u[x-i+n]=0;
            v[x+i]=0;
        }
    }
}

int main(){
    cin>>n;
    dfs(1);
    cout<<Count<<endl;
}

迷宫

题目背景
给定一个N*M方格的迷宫，迷宫里有T处障碍，障碍处不可通过。给定起点坐标和终点坐标，问: 每个方格最多经过1次，有多少种从起点坐标到终点坐标的方案。在迷宫中移动有上下左右四种方式，每次只能移动一个方格。数据保证起点上没有障碍。

题目描述
无

输入格式
第一行N、M和T，N为行，M为列，T为障碍总数。第二行起点坐标SX,SY，终点坐标FX,FY。接下来T行，每行为障碍点的坐标。

输出格式
给定起点坐标和终点坐标，问每个方格最多经过1次，从起点坐标到终点坐标的方案总数。

输入

2 2 1
1 1 2 2
1 2

输出

1

#include<iostream>

using namespace std;
int n,m,t,sx,sy,fx,fy,Count=0;
int Map[10][10];//相当于vis数组
int way[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
void dfs(int x,int y){
    if(x==fx&&y==fy){
        Count++;
        return;
    }
    for(int i=0;i<4;i++){
        int dx=x+way[i][0];
        int dy=y+way[i][1];
        if(dx>=1&&dx<=n&&dy>=1&&dy<=n&&!Map[dx][dy]){
            Map[dx][dy]=1;
            dfs(dx,dy);
            Map[dx][dy]=0;
        }
    }
}


int main(){
    cin>>n>>m>>t>>sx>>sy>>fx>>fy;
    while(t--){
        int x,y;
        cin>>x>>y;
        Map[x][y]=1;
    }
    Map[sx][sy]=1;
    dfs(sx,sy);
    cout<<Count<<endl;
}

单词方阵

题目描述
给一n×n的字母方阵，内可能蕴含多个“yizhong”单词。单词在方阵中是沿着同一方向连续摆放的。摆放可沿着 8 个方向的任一方向，同一单词摆放时不再改变方向，单词与单词之间可以交叉,因此有可能共用字母。输出时，将不是单词的字母用*代替，以突出显示单词。例如：
在这里插入图片描述
输入格式
第一行输入一个数nn。(7 \le n \le 1007≤n≤100)。

第二行开始输入n \times nn×n的字母矩阵。

输出格式
突出显示单词的n \times nn×n矩阵。

输入

8
qyizhong
gydthkjy
nwidghji
orbzsfgz
hhgrhwth
zzzzzozo
iwdfrgng
yyyygggg

输出

yizhong
gy**
ni****
oz**
hh
z**o
i*****n
y**g

#include<iostream>

using namespace std;
char Map[300][300];
int vis[300][300];
int way[8][2]={{0,1},{0,-1},{1,0},{-1,0},{1,1},{1,-1},{-1,1},{-1,-1}};
string yz="yizhong";//是从i开始比较
int n;
void dfs(int x,int y){
    for(int i=0;i<8;i++){//8个方向
        bool flag=true;
        for(int j=1;j<=6;j++){//需要比较的6，也相当于走的步数
            int dx=x+j*way[i][0];
            int dy=y+j*way[i][1];
            if(!(dx>=1&&dx<=n&&dy>=1&&dy<=n)||yz[j]!=Map[dx][dy]){
                flag=false;
            }
        }
        if(flag){
            for(int j=0;j<7;j++){
                int dx=x+j*way[i][0];
                int dy=y+j*way[i][1];
                vis[dx][dy]=1;
            }
        }
    }
}

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>Map[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(Map[i][j]=='y'){
                dfs(i,j);
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(vis[i][j]==1) cout<<Map[i][j];
            else cout<<'*';
        }
        cout<<endl;
    }
}