论文

2021-01-12

题目描述
小H为了完成一篇论文，一共要完成n个实验。其中第i个实验需要ai的时间去完成。小H可以同时进行若干实验，但存在一些实验，只有当它的若干前置实验完成时，才能开始进行该实验。同时我们认为小H在一个实验的前置实验都完成时，就能马上开始该实验。为了让小H尽快完成论文，需要知道在最优的情况下，最后一个完成的实验什么时候完成？小H还想知道，在保证最后一个实验尽快完成的情况下（即保证上一问的答案不变），他想知道每个实验最晚可以什么时候开始。设第i个实验最早可能的开始时间为fi，不影响最后一个实验完成时间的最晚开始时间为gi，请你证明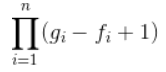除以10^9+7所得的余数。题目保证有解。

输入描述:
从标准输入读入数据。
第一行输入一个整数n，m。
第二行输入n个正整数，a1,a2,…..an,描述每个实验完成所需要的时间。
接下来读入m行，每行读入两个整数u,v，表示编号为u的实验是编号为v的实验的前置实验。
对于所有的输入数据，都满足1<=n<=10^5,1<=m<=510^5,1<=ai<=10^6。
*输出描述:**
输出到标准输出。
第一行输出一个整数表示最晚完成的实验的时间。
第二行输出一个整数表示除以10^9+7所得的余数。
输入输出样例
输入样例#:

7 5
11 20 17 10 11 17 17
5 4
6 1
7 3
2 4
2 1

输出样例#:

34
7840

提示：
第一个点最早开始时间为20，最晚开始时间为23。
第二个点最早开始时间为0，最晚开始时间为3。
第三个点最早开始时间为17，最晚开始时间为17。
第四个点最早开始时间为20，最晚开始时间为24。
第五个点最早开始时间为0，最晚开始时间为13。
第六个点最早开始时间为0，最晚开始时间为6。
第七个点最早开始时间为0，最晚开始时间为0。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<climits>

using namespace std;

const int MAXN=1e5+7;
const int INF=INT_MAX;
const int MOD=1e9+7;


vector<int> graph[MAXN];//邻接表
long long earliest[MAXN];//最早开始时间
long long latest[MAXN];//最晚开始时间
long long time[MAXN];//花费时间
int inDegree[MAXN];

long long CriticalPath(int n){
    vector<int> topology;//拓扑序列
    queue<int> node;
    for(int i=1;i<=n;i++){
        if(inDegree[i]==0){
            node.push(i);
        }
    }
    long long totalTime=0;//总耗时
    while(!node.empty()){
        int u=node.front();
        topology.push_back(u);
        node.pop();
        for(int i=0;i<graph[u].size();i++){
            int v=graph[u][i];
            earliest[v]=max(earliest[v],earliest[u]+time[u]);//正向找最大，形成earliest
            inDegree[v]--;
            if(inDegree[v]==0){
                node.push(v);
                totalTime=max(totalTime,earliest[v]+time[v]);
            }
        }
    }
    for(int i=topology.size()-1;i>=0;i--){
        int u=topology[i];
        if(graph[u].size()==0) latest[u]=totalTime-time[u];//汇点的最晚开始时间初始化
        else latest[u]=INF;//非汇点的最晚开始时间的初始化
        for(int j=0;j<graph[u].size();j++){
            int v=graph[u][j];
            latest[u]=min(latest[u],latest[v]-time[u]);//逆向找最小，形成latest
        }
    }
    return totalTime;
}

int main(){
    int n,m;
    while(cin>>n>>m){
        memset(graph,0,sizeof(graph));
        memset(earliest,0,sizeof(earliest));
        memset(latest,0,sizeof(latest));
        memset(inDegree,0,sizeof(inDegree));
        memset(time,0,sizeof(time));
        for(int i=1;i<=n;i++){
            cin>>time[i];
        }
        while(m--){
            int from,to;
            cin>>from>>to;
            graph[from].push_back(to);
            inDegree[to]++;
        }
        long long totalTime=CriticalPath(n);
        long long answer=1;
        for(int i=1;i<=n;i++){
            answer*=latest[i]-earliest[i]+1;
            answer%=MOD;
        }
        cout<<totalTime<<endl;
        cout<<answer<<endl;
    }
}