导语
常见的背包问题有
1、组合问题: dp[i] += dp[i-num]
2、True、False问题:dp[i] = dp[i] or dp[i-num]
3、最大最小问题:dp[i] = min(dp[i], dp[i-num]+1)
dp[i] = max(dp[i], dp[i-num]+1)
注意dp的初始化!!!
0-1背包
1.采药问题
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
第一行有2个整数T(1≤T≤1000)和M(1≤M≤100),用一个空格隔开,T代表总共能够用来采药的时间,M代表山洞里的草药的数目。
接下来的M行每行包括两个在1到100之间(包括1和100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
1个整数,表示在规定的时间内可以采到的草药的最大总价值。
输入输出样例
输入
70 3
71 100
69 1
1 2
输出
3
分析
普通的0-1背包,求最大的收益
#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=1000;
int w[MAXN],v[MAXN];
int dp[MAXN];
int main(){
int n,m;//容量为n,物品有m个
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>w[i]>>v[i];
}
for(int i=1;i<=m;i++){//上到下,关于第i个物品选与不选
for(int j=n;j>=w[i];j--){//右到左,关于选与不选对应的收益
dp[j]=max(dp[j-w[i]]+v[i],dp[j]);
}
}
cout<<dp[n]<<endl;
}
2.装箱问题
题目描述
有一个箱子容量为V(200000≤V≤20000),同时有n个物品(300<n≤30),每个物品有一个体积(正整数)。
要求n个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
输入格式
1个整数,表示箱子容量
1个整数,表示有n个物品
接下来n行,分别表示这n个物品的各自体积
输出格式
1个整数,表示箱子剩余空间。
输入
24 6
8
3
12
7
9
7
输出
0
分析
注意分析什么是模板中的变量的转换,比如什么是背包容量,什么是价值,什么是重量,这道题转化为求装入若干个物品使其体积和最大
#include<iostream>
using namespace std;
const int MAXN=50;
int w[MAXN],v[MAXN];
int dp[30005];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>w[i];
v[i]=w[i];//这个题的物品重量等同于价值
}
for(int i=1;i<=m;i++){
for(int j=n;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout<<n-dp[n]<<endl;
}
3.最大约数和
题目描述
选取和不超过S的若干个不同的正整数,使得所有数的约数(不含它本身)之和最大。
输入格式
输入一个正整数S。
输出格式
输出最大的约数之和。
输入
11
输出
9
说明/提示
取数字4和6,可以得到最大值(1+2)+(1+2+3)=9。
#include<iostream>
using namespace std;
const int MAXN=2000;
int v[MAXN];
int dp[10000];
int main(){
int n,m;
cin>>m;
n=m;
for(int i=1;i<=m;i++){
for(int j=1;j<i;j++){
if(i%j==0) v[i]+=j;
}
//cout<<i<<":"<<v[i]<<endl;
}
for(int i=1;i<=m;i++){
for(int j=n;j>=i;j--){
dp[j]=max(dp[j],dp[j-i]+v[i]);//数字本身为重量,数字的约数之和为价值
}
}
cout<<dp[n]<<endl;
}4.精卫填海
题目描述
发鸠之山,其上多柘木。有鸟焉,其状如乌,文首,白喙,赤足,名曰精卫,其名自詨。是炎帝之少女,名曰女娃。女娃游于东海,溺而不返,故为精卫。常衔西山之木石,以堙于东海。——《山海经》
精卫终于快把东海填平了!只剩下了最后的一小片区域了。同时,西山上的木石也已经不多了。精卫能把东海填平吗?
事实上,东海未填平的区域还需要至少体积为v的木石才可以填平,而西山上的木石还剩下n块,每块的体积和把它衔到东海需要的体力分别为k和m。精卫已经填海填了这么长时间了,她也很累了,她还剩下的体力为c。
输入格式
输入文件的第一行是三个整数:v、n、c。
从第二行到第n+1行分别为每块木石的体积和把它衔到东海需要的体力。
输出格式
输出文件只有一行,如果精卫能把东海填平,则输出她把东海填平后剩下的最大的体力,否则输出’Impossible’(不带引号)。
输入
100 2 10
50 5
50 5
输出
0
输入
10 2 1
50 5
10 2
输出
Impossible
分析
这道题稍微有点不同,这道题是算背包容量能剩下多少,所以在计算出各个dp后,要背包容量从1开始递增看是否能够满足,然后输出剩下的最大体力.
#include<iostream>
using namespace std;
const int MAXN=10005;
int w[MAXN]; int v[MAXN];
int dp[20000];
int main(){
int s,m,n;//s为剩下没填的体积,m为物品件数,n为背包容量
cin>>s>>m>>n;
for(int i=1;i<=m;i++){
cin>>v[i]>>w[i];
}
for(int i=1;i<=m;i++){
for(int j=n;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);//计算当前剩余体力能搬的最大体积数
}
}
for(int i=1;i<=n;i++){//遍历各个背包容量
if(dp[i]>=s) {cout<<n-i<<endl; return 0;}
}
//if(dp[n]>=s) cout<<dp[n]-s<<endl; //错误,因为在之前就可能已经满足了,没求到剩下的最大体力
cout<<"Impossible"<<endl;
return 0;
}
5.集合 Subset Sums(组合数)
题目描述
对于从 1∼n 的连续整数集合,能划分成两个子集合,且保证每个集合的数字和是相等的。举个例子,如果 n=3,对于{1,2,3} 能划分成两个子集合,每个子集合的所有数字和是相等的:{3} 和 {1,2} 是唯一一种分法(交换集合位置被认为是同一种划分方案,因此不会增加划分方案总数)如果n=7,有四种方法能划分集合 {1,2,3,4,5,6,7},每一种分法的子集合各数字和是相等的:
{1,6,7} 和 {2,3,4,5}
{2,5,7} 和 {1,3,4,6}
{3,4,7} 和 {1,2,5,6}
{1,2,4,7} 和 {3,5,6}
给出 n,你的程序应该输出划分方案总数。
输入格式
输入文件只有一行,且只有一个整数 n
输出格式
输出划分方案总数。
输入
7
输出
4
分析
方法类的背包问题,注意背包容量是总的和的一半,而最终求的是划分而不是集合,所以要除以2
#include<iostream>
using namespace std;
const int MAXN=100;
long long dp[1000]={1};//方法种类的背包问题,初始化为1
int main(){
int m,n;
cin>>m;
n=m;//n为物品数
if((1+m)*m/2%2==0) m=(1+m)*m/2;//总的和,其一半是背包的容量
else{
cout<<0; return 0;
}
for(int i=1;i<=n;i++){
for(int j=m/2;j>=i;j--){
dp[j]=dp[j]+dp[j-i];//选与不选
}
}
cout<<dp[m/2]/2<<endl;//因为求的是划分数而不是和为m/2的集合数
}
6.目标和

设P为正数集的和,N为负数集合的和,S为所有元素和,T为目标和
∵P+N=S
P-N=T
∴2P=S+T
所以只要找到在序列找到和为(S+T)/2的所有方案就行,此时转化成了0-1背包的组合数问题
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int S) {
int n=nums.size();
int sum=0;
for(int i=0;i<n;i++){
sum+=nums[i];
}
long long temp=(long long)sum+(long long)S;
if(temp%2==1||S-sum>0) return 0;
int target=(sum+S)/2;
//初始化
vector<int> dp(10010,0);
dp[0]=1;;
//cout<<dp[S]<<endl;
for(int i=0;i<n;i++){
for(int j=target;j>=nums[i];j--){
//cout<<j<<" "<<j-nums[i]<<endl;
dp[j]=dp[j]+dp[j-nums[i]];
//cout<<dp[j]<<endl;
}
}
return dp[target];
}
};7.分割等和子集(true&false)

class Solution {
public:
long long dp[10010];
bool canPartition(vector<int>& nums) {
int sum=0;
for(int i=0;i<nums.size();i++){
sum+=nums[i];
}
if(sum%2==1) return false;
int target=sum/2;
//初始化,注意初始化的方法
vector<bool> dp(target,false);
dp[0]=true;
cout<<dp[0]<<endl;
for(int i=0;i<nums.size();i++){
for(int j=target;j>=nums[i];j--){
dp[j]=dp[j]||dp[j-nums[i]];
//cout<<dp[j]<<endl;
}
}
return dp[target];
}
};8.一和零(双weight)

注:这里的weight是二维的(对于每一个串都有自己0,1的weight)
int findMaxForm(vector<string>& strs, int m, int n) {
//dp[i][j]表示i个0,j个1能够拼出的数组中的最大的字符串数量
vector<vector<int>> dp(m+1,vector<int>(n+1));
vector<vector<int>> weight(strs.size(),vector<int>(2,0));
//cout<<dp[1][1]<<endl;
for(int i=0;i<strs.size();i++){
for(int j=0;j<strs[i].size();j++){
if(strs[i][j]=='0') weight[i][0]++;
else weight[i][1]++;
}
//cout<<weight[i][0]<<" "<<weight[i][1]<<endl;
}
for(int k=0;k<strs.size();k++){//从上到下每个物品选与不选
//cout<<weight[k][0]<<" "<<weight[k][1]<<endl;
for(int i=m;i>=weight[k][0];i--){//遍历0的背包容量
for(int j=n;j>=weight[k][1];j--){//遍历1的背包容量
dp[i][j]=max(dp[i][j],dp[i-weight[k][0]][j-weight[k][1]]+1);
//cout<<dp[i][j]<<endl;
}
}
}
return dp[m][n];
}完全背包
1.疯狂的采药
题目描述
LiYuxiang是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同种类的草药,采每一种都需要一些时间,每一种也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是LiYuxiang,你能完成这个任务吗?
此题和原题的不同点:
1.每种草药可以无限制地疯狂采摘。
2.药的种类眼花缭乱,采药时间好长好长啊!师傅等得菊花都谢了!
输入格式
输入第一行有两个整数T(1 <= T <= 100000)和M(1 <= M <= 10000),用一个空格隔开,T代表总共能够用来采药的时间,M代表山洞里的草药的数目。接下来的M行每行包括两个在1到10000之间(包括1和10000)的整数,分别表示采摘某种草药的时间和这种草药的价值。
输出格式
输出一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
输入
70 3
71 100
69 1
1 2
输出
140
分析
完全背包要修改j的遍历方式,需要反着来
#include<iostream>
using namespace std;
const int MAXN=10005;
int w[MAXN],v[MAXN];
int dp[100005];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>w[i]>>v[i];
}
for(int i=1;i<=m;i++){
for(int j=w[i];j<=n;j++){//完全背包和0-1背包这里是反着的
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout<<dp[n]<<endl;
}
2.神奇的四次方数
题目描述
将一个整数m分解为n个四次方数的和的形式,要求n最小。例如,m=706,706=5^4+3^4,则n=2。
输入格式
一行,一个整数m。
输出格式
一行,一个整数n。
输入
706
输出
2
分析
这道题因为求的是最小,所以要将dp初始化为一个比较大的数,并且dp[0]=0;
相当于给一个初始值,含义为容量为0时最少选择0个数.
#include<iostream>
#include<cstring>
#include<math.h>
using namespace std;
const int MAXN=100;
int w[MAXN];//每个的w都是1
int dp[1000001];
int main(){
//下面这两步一定要写
memset(dp,63,sizeof(dp));
//给了一个初始值,不然结果会是一个很大的数,其含义代表容量为0时最少选择0个数
dp[0]=0;
int n,m;//n为背包容量
cin>>n;
for(int i=1;pow(i,4)<=n;i++){
w[i]=i*i*i*i;
m=i;//m表示物品的数目
}
for(int i=1;i<=m;i++){
for(int j=w[i];j<=n;j++){//v[i]是1
dp[j]=min(dp[j],dp[j-w[i]]+1);
// cout<<dp[j]<<endl;
}
}
cout<<dp[n]<<endl;
}
3.零钱兑换 II(组合数)
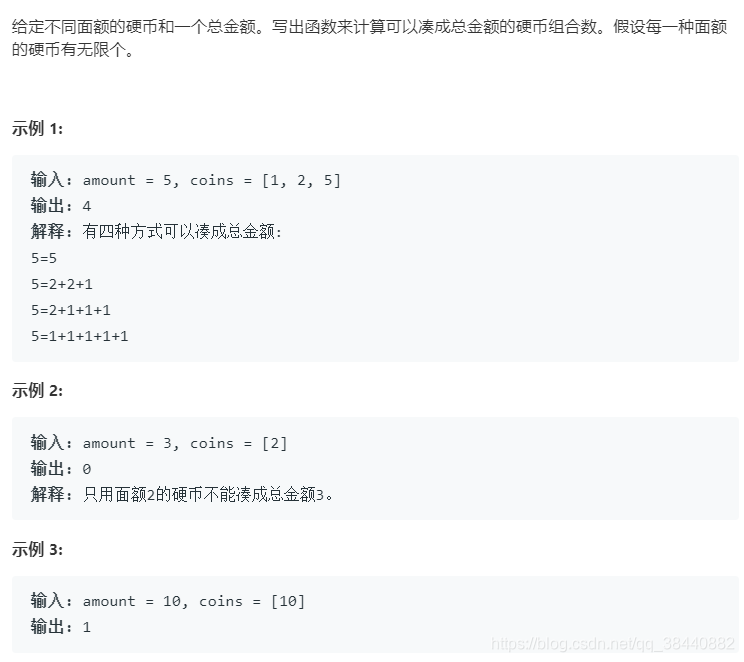
是求组合数,因为{1,2},{2,1}是同一个
求组合数模板是先遍历物品,再遍历背包
class Solution {
public:
int dp[10010];
int change(int amount, vector<int>& coins) {
memset(dp,0,sizeof(dp));
dp[0]=1;
for(int i=0;i<coins.size();i++){
for(int j=coins[i];j<=amount;j++){
dp[j]=dp[j]+dp[j-coins[i]];
}
}
return dp[amount];
}
};4.组合总和 Ⅳ(排列数,反向嵌套)

是求排列数,因为{1,2},{2,1}不是同一个
求组合数模板是先遍历背包,再遍历物品
class Solution {
public:
int combinationSum4(vector<int>& nums, int target)
{
if(nums.size() == 0)
return 0;
vector<unsigned int> dp(target + 1, 0);
dp[0] = 1;//组成0的方案只能是全部都不选择,所以方案数为1.
for(int i = 0; i <= target; i++)
{
for(int j = 0; j < nums.size(); j++)
{
if(i - nums[j] >= 0)
dp[i] += dp[i - nums[j]];
}
}
return dp[target];
}
};
分组背包
1.通天之分组背包
题目描述
自01背包问世之后,小A对此深感兴趣。一天,小A去远游,却发现他的背包不同于01背包,他的物品大致可分为k组,每组中的物品相互冲突,现在,他想知道最大的利用价值是多少。
输入格式
两个数m,n,表示一共有n件物品,总重量为m
接下来n行,每行3个数ai,bi,ci,表示物品的重量,利用价值,所属组数
输出格式
一个数,最大的利用价值
输入
45 3
10 10 1
10 5 1
50 400 2
输出
10
分析
分组背包采用结构体数组,其下标代表组数,内部的w,v数组存的是组内的元素情况,总组数要在输入中算出,第二次遍历也是先遍历所有组,其本质相当于0-1背包的问题
#include<iostream>
using namespace std;
const int MAXN=2000;
struct group{
int group_size;//组的大小
int w[MAXN],v[MAXN];
}G[1000];//下标代表组号
int dp[10000];
int main(){
int n,m,s=0;//s代表组数
cin>>n>>m;
for(int i=1;i<=m;i++){
int a,b,c;
cin>>a>>b>>c;
s=max(c,s);//统计总的组数
G[c].group_size++;//c组内的成员增加
int ci=G[c].group_size;
G[c].w[ci]=a;
G[c].v[ci]=a;
}
for(int i=1;i<=s;i++){//从上到下遍历所有组
for(int j=n;j>=0;j--){
for(int k=1;k<=G[i].group_size;k++){//组内成员竞争,注意j不会变化
if(j-G[i].w[k]>=0){//注意
dp[j]=max(dp[j],dp[j-G[i].w[k]]+G[i].v[k]);
}
}
}
}
cout<<dp[n]<<endl;
}
2.金明的预算方案
题目描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过NN元钱就行”。今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
主件 附件
电脑 打印机,扫描仪
书柜 图书
书桌 台灯,文具
工作椅 无
如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有0个、1个或2个附件。附件不再有从属于自己的附件。金明想买的东西很多,肯定会超过妈妈限定的N元。于是,他把每件物品规定了一个重要度,分5等:用整数1−5表示,第5等最重要。他还从因特网上查到了每件物品的价格(都是10元的整数倍)。他希望在不超过N元(可以等于N元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
请你帮助金明设计一个满足要求的购物单。
输入格式
第11行,为两个正整数,用一个空格隔开:
n m(其中N(<32000)表示总钱数,m(<60)为希望购买物品的个数。) 从第2行到第m+1行,第j行给出了编号为j−1的物品的基本数据,每行有3个非负整数
v p q(其中v表示该物品的价格(v<10000),p表示该物品的重要度(1-5),q表示该物品是主件还是附件。如果q=0,表示该物品为主件,如果q>0,表示该物品为附件,q是所属主件的编号)
输出格式
一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(<200000)。
输入
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
输出
2200
分析
先转化为分组问题,假设有主(①),从(②),从(③)
所以得到一个组内四个相斥的成员:
①、①②、①③、①③
#include<iostream>
using namespace std;
const int MAXN=100;
struct group{
int group_size;
int w[MAXN],v[MAXN];
}G[2000];
int dp[32005];
//因为每个主件可以有0个、1个或2个附件,所以对于组内只有四种相互排斥的情况,所以可以转化为分组背包
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
int v,p,q;
cin>>v>>p>>q;
if(q==0){//是这组的第一个,i就代表了组号
G[i].group_size=1;
G[i].w[1]=v;
G[i].v[1]=p*v;
}
else{
if(G[q].group_size==1){//一主一从,q代表所从属的组
G[q].group_size=2;
G[q].w[2]=G[q].w[1]+v;//一个主,从一号
G[q].v[2]=G[q].v[1]+p*v;
}
else{
G[q].group_size=4;//
G[q].w[3]=G[q].w[1]+v;//一个主,从二号
G[q].v[3]=G[q].v[1]+p*v;
G[q].w[4]=G[q].w[2]+v;//一个主,从一号,从二号
G[q].v[4]=G[q].v[2]+p*v;
}
}
}
for(int i=1;i<=m;i++){//遍历所有组
for(int j=n;j>=0;j--){
for(int k=1;k<=G[i].group_size;k++){//组内成员竞争
if(j>=G[i].w[k]){//
dp[j]=max(dp[j],dp[j-G[i].w[k]]+G[i].v[k]);
//cout<<dp[j]<<endl;
}
}
}
}
cout<<dp[n]<<endl;
}