动态规划总结

简单dp

最大连续子序列

三角形最小路径和

class Solution {
public:


    int minimumTotal(vector<vector<int>>& triangle) {
        int m=triangle.size();
        vector<vector<int>> dp(m,vector<int> (m,INT_MAX));
        int ans=INT_MAX;
        for(int i=0;i<m;i++){
            for(int j=0;j<=i;j++){
                if(i==0&&j==0){
                    dp[i][j]=triangle[i][j];
                    continue;
                }
                //上和左上的值，即上一步的位置
                int up=INT_MAX,left_up=INT_MAX;
                if(i>=j){//此时上方存在元素
                    up=dp[i-1][j];
                }
                if(j-1>=0){////此时左上方存在元素
                    left_up=dp[i-1][j-1];
                }
                dp[i][j]=min(up,left_up)+triangle[i][j];
                //cout<<i<<" "<<j<<":"<<dp[i][j]<<endl;
            }
        }
        //遍历最后一行，找到总路径和最小的出口
        for(int j=0;j<triangle[m-1].size();j++){
            if(dp[m-1][j]<ans) ans=dp[m-1][j];
        }
        return ans;
    }
};

最长递增子序列

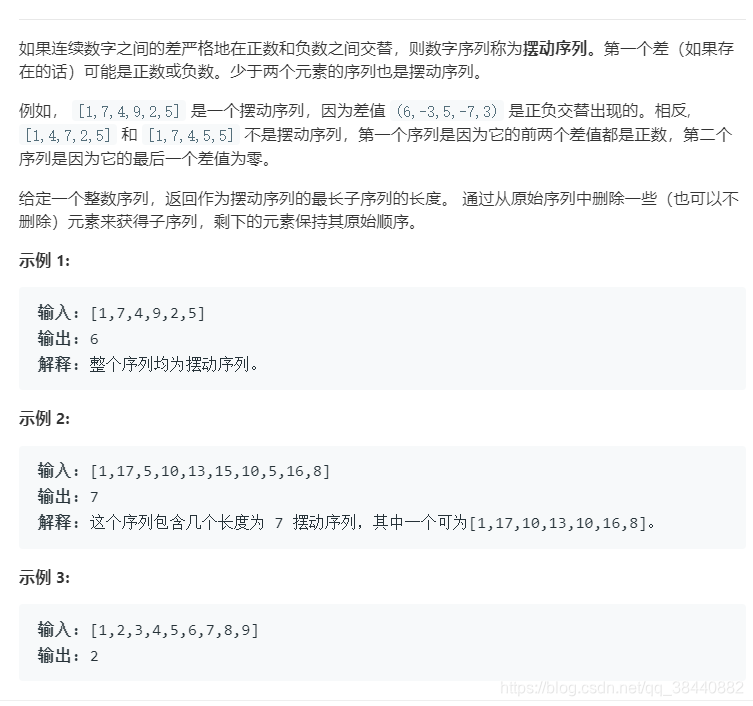
摆动序列

class Solution {
public:
    //up[i] 存的是目前为止最长的以第 i 个元素结尾的上升摆动序列的长度。

    //down[i] 记录的是目前为止最长的以第 i 个元素结尾的下降摆动序列的长度。

    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size();
        if(n==0) return 0;
        vector<int> up(n,1);
        vector<int> down(n,1);
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j]){
                    up[i]=max(up[i],down[j]+1);
                }
                else if(nums[i]<nums[j]){
                    down[i]=max(down[i],up[j]+1);
                }
                //cout<<nums[i]<<endl;
                //cout<<up[i]<<" "<<down[i]<<endl;
            }
        }
        return max(up[n-1],down[n-1]);
    }
};

最长公共子序列

背包问题

区间dp

戳气球

树型dp

打家劫舍 III

class Solution {
public:
    int rob(TreeNode* root) {
        auto ans=dfs(root);
        return max(ans.first,ans.second);
    }

    //返回的pair->first:选择当前结点的最大收益;pair->second:不选当前结点的最大收益
    pair<int,int> dfs(TreeNode* root){
        if(root==NULL) return {0,0};
        auto left_pair=dfs(root->left);
        auto right_pair=dfs(root->right);
        //选root|不选root
        return {root->val+left_pair.second+right_pair.second,
                //max(选左边，不选左边)+max(选右边，不选右边)
                max(left_pair.first,left_pair.second)+max(right_pair.first,right_pair.second)};
    }
};

二叉树中的最大路径和

class Solution {
public:
    int maxh;
    //因为有全部是负数的树存在(因为对NULL的处理是返回{0,0})，所以对这个情况单独拿出来
    bool all_negetive=true;
    int max_negetive=INT_MIN;
    int max_path=INT_MIN;
    int maxPathSum(TreeNode* root) {
        auto ans=dfs(root);
        //if(root->left==NULL&&root->right==NULL) return root->val;
        if(all_negetive){
            return max_negetive;
        }
        else return max_path;
    }
    pair<int,int> dfs(TreeNode* root){
        if(root==NULL){
            return {0,0};
        }
        if(root->val>=0) all_negetive=false;
        max_negetive=max(max_negetive,root->val);
        auto left_pair=dfs(root->left);
        auto right_pair=dfs(root->right);
        //cout<<root->val<<endl;
        //cout<<left_pair.first<<" "<<left_pair.second<<endl;
        //cout<<right_pair.first<<" "<<right_pair.second<<endl;
        max_path=max(max_path,
                    max(
                        max(root->val+left_pair.first,
                            root->val+right_pair.first),
                        max(root->val,
                            root->val+left_pair.first+right_pair.first)
                    )
                );
        return {
//选root,要注意路径里面的结点是连续的,比如如果左边儿子没有选，那么不选左边儿子的最大路径和与当前结点的最大路径和也没关系了
//并且子节点不能左右都选，不然就不是路径,所以当要选儿子时，最多只会选择儿子一条边来与自己构成路径
        max(max(root->val+left_pair.first,root->val),root->val+right_pair.first),
            //不选root
        max(max(left_pair.first,left_pair.second),max(right_pair.first,right_pair.second))
        };
    }

};

数位dp

题目描述
不要49

//    pos    = 当前处理的位置(一般从高位到低位)
//    pre    = 上一个位的数字(更高的那一位)
//    status = 要达到的状态,如果为1则可以认为找到了答案,到时候用来返回,
//         　　 给计数器+1。
//    limit  = 是否受限,也即当前处理这位能否随便取值。如567,当前处理6这位,
//         　　 如果前面取的是4,则当前这位可以取0-9。如果前面取的5,那么当前
//         　　 这位就不能随便取，不然会超出这个数的范围,所以如果前面取5的
//         　　 话此时的limit=1,也就是说当前只可以取0-6。
//
//    用DP数组保存这三个状态是因为往后转移的时候会遇到很多重复的情况。
int    dfs(int pos,int pre,int status,int limit)
{
    //已结搜到尽头,返回"是否找到了答案"这个状态。
    if(pos < 1)
        return    status;

    //DP里保存的是完整的,也即不受限的答案,所以如果满足的话,可以直接返回。
    if(!limit && DP[pos][pre][status] != -1)
        return    DP[pos][pre][status];

    int    end = limit ? DIG[pos] : 9;
    int    ret = 0;

    //往下搜的状态表示的很巧妙,status用||是因为如果前面找到了答案那么后面
    //还有没有答案都无所谓了。而limti用&&是因为只有前面受限、当前受限才能
    //推出下一步也受限，比如567,如果是46X的情况,虽然6已经到尽头,但是后面的
    //个位仍然可以随便取,因为百位没受限,所以如果个位要受限,那么前面必须是56。
    //
    //这里用"不要49"一题来做例子。
    for(int i = 0;i <= end;i ++)
        ret += dfs(pos - 1,i,status || (pre == 4 && i == 9),limit && (i == end));

    //DP里保存完整的、取到尽头的数据
    if(!limit)
        DP[pos][pre][status] = ret;

    return    ret;
}

其他

把数字翻译成字符串

题目描述
给定一个数字，按照如下规则翻译成字符串：0 翻译成“a”，1 翻译成“b”… 25 翻译成“z”。一个数字有多种翻译可能，例如 12258 一共有 5 种，分别是 bccfi，bwfi，bczi，mcfi，mzi。实现一个函数，用来计算一个数字有多少种不同的翻译方法。

public class Solution {
    public int numDecodings(String s) {
        if(s == null || s.length() == 0) {
            return 0;
        }
        int n = s.length();
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = s.charAt(0) != '0' ? 1 : 0;
        for(int i = 2; i <= n; i++) {
            int first = Integer.valueOf(s.substring(i-1, i));
            int second = Integer.valueOf(s.substring(i-2, i));
            if(first >= 1 && first <= 9) {
               dp[i] += dp[i-1];  
            }
            if(second >= 10 && second <= 26) {
                dp[i] += dp[i-2];
            }
        }
        return dp[n];
    }
}

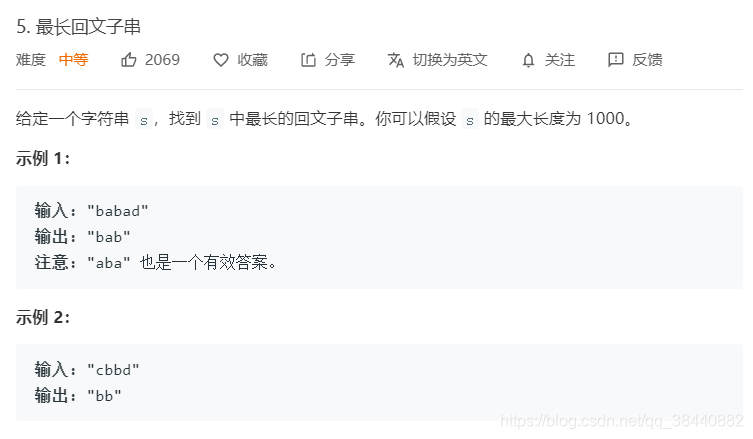
最长回文子串

class Solution {
public:
    int Max=0;
    string longestPalindrome(string s) {
        int n=s.size();
        vector<vector<bool>> dp(n,vector<bool>(n));
        //dp[j][i]表示从j到i是否为回文子串
        string ans;
        if(s.size()==0) return "";
        else if(s.size()==1) return s;
        for(int i=0;i<s.size();i++){
            for(int j=i;j>=0;j--){
                if(s[i]==s[j]&&(i-j<=2||dp[j+1][i-1])){
                    dp[j][i]=true;
                    if(i-j+1>Max){
                        ans=s.substr(j,i-j+1);
                        Max=i-j+1;
                    }
                }
            }
        }
        return ans;
    }
};

正则表达式匹配

class Solution {
public:
    bool isMatch(string s, string p) {
        s=" "+s;//防止该案例：""\n"c*"
        p=" "+p;
        int m=s.size(),n=p.size();
        bool dp[m+1][n+1];
        memset(dp,false,(m+1)*(n+1));
        dp[0][0]=true;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(s[i-1]==p[j-1] || p[j-1]=='.'){
                    dp[i][j]=dp[i-1][j-1];
                }
                else if(p[j-1]=='*'){
                    if(s[i-1]!=p[j-2] && p[j-2]!='.')
                        dp[i][j]=dp[i][j-2];
                    else{
                        dp[i][j]=dp[i][j-1] || dp[i][j-2] || dp[i-1][j];

                    }
                }
            }
        }
        return dp[m][n];
    }
};

最长有效括号

注意：进行括号匹配的时候分三段:
1.前一个字符结尾能匹配的最长的串
2.能和当前这个字符匹配的 (
3.再往前一个能匹配的最长串

class Solution {
public:
    int longestValidParentheses(string s) {
        if(s.size()==0) return 0;
        int n=s.size();
        int max_len=0;
        vector<int>  dp(n);//dp[i]表示以s[i]结尾的最长有效括号长度
        dp[0]=0;
        for(int i=0;i<s.size();i++){
            if(s[i]=='(') dp[i]=0;
            else{
                if(i>=1&&s[i-1]=='('){//      ()的情况
                    if(i==1) dp[i]=2;
                    else{
                        dp[i]=dp[i-2]+2;
                    }
                }
                else if(i>=1&&s[i-1]==')'){//  ))的情况
                    //cout<<i<<" "<<dp[i-1]<<endl;
                    if(i-dp[i-1]-1<0||s[i-dp[i-1]-1]!='(') dp[i]=0;
                    else if(s[i-dp[i-1]-1]=='('){

                        if(i-dp[i-1]-2<0){
                            dp[i]=0+dp[i-1]+2;
                        }
                        else{
                            dp[i]=dp[i-dp[i-1]-2]+dp[i-1]+2;
                        }
                    }
                }
            }
            cout<<dp[i]<<endl;
            max_len=max(max_len,dp[i]);
        }
        return max_len;
    }
};

编辑距离

class Solution {
public:
    int dp[666][666];
    int minDistance(string word1, string word2) {
        int m=word1.size();
        int n=word2.size();
        //cout<<m<<endl;
        word1=" "+word1;
        word2=" "+word2;
        //只进行删除的状态
        for(int i=0;i<word1.size();i++){
            dp[i][0]=i;
        }
        //只进行插入的状态
        for(int j=0;j<word2.size();j++){
            dp[0][j]=j;
        }
        //自顶向下
        for(int i=1;i<=word1.size();i++){
            for(int j=1;j<=word2.size();j++){
                //相同则不做操作
                if(word1[i]==word2[j]){
                    dp[i][j]=dp[i-1][j-1];
                }
                else{
                    dp[i][j]=Min(
                        dp[i][j-1]+1,//插入
                        dp[i-1][j]+1,//删除
                        dp[i-1][j-1]+1//替换
                    );
                }
                //cout<<i<<","<<j<<":"<<dp[i][j]<<endl;
            }
        }
        return dp[m][n];
    }


    int Min(int x,int y,int z){
        return min(x,min(y,z));
    }
};

最大正方形

class Solution {
public:

    struct node{
        int rows,cols;
        //方便初始化
        node():rows(0),cols(0){}
    };
    int max_Area=0;
    int maximalSquare(vector<vector<char>>& matrix) {
        int m=matrix.size();
        if(m==0) return 0;
        int n=matrix[0].size();
        vector<vector<node>> dp(m+1,vector<node>(n+1,node()));
        if(matrix[0][0]=='1'){
            dp[0][0].rows=1;
            dp[0][0].cols=1;
        }
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(i==0||j==0){
                    dp[i][j].rows=matrix[i][j]-'0';
                    dp[i][j].cols=matrix[i][j]-'0';                    
                }
                else if(matrix[i][j]=='1'){
                    dp[i][j].rows=min(dp[i-1][j-1].rows,dp[i][j-1].rows)+1;
                    dp[i][j].cols=min(dp[i-1][j-1].cols,dp[i-1][j].cols)+1;
                }
                //cout<<i<<","<<j<<"   "<<dp[i][j].rows<<" "<<dp[i][j].cols<<endl;
            }
        }
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                int edge=min(dp[i][j].rows,dp[i][j].cols);
                max_Area=max(max_Area,edge*edge);
            }
        }
        return max_Area;
    }
};

赏

谢谢你请我吃糖果